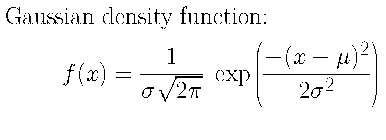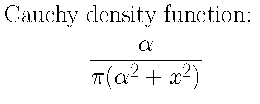Random Distributions
In the algorithms below, random() generates a random number
in the range from 0.0 to 1.0 inclusive.
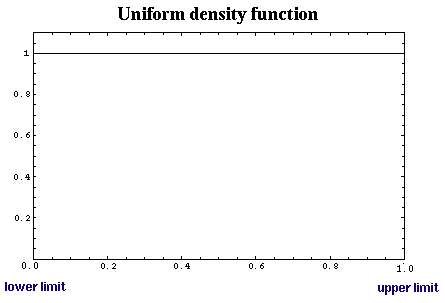
Uniform Distribution
Linear Distribution
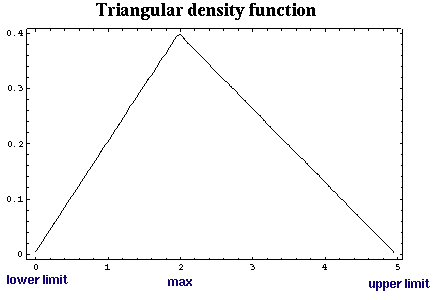
Triangular Distribution
Exponential Distribution
Bilateral Distribution
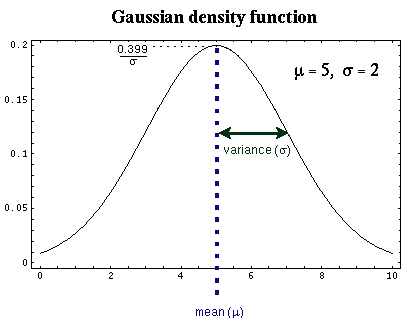
Gaussian Distribution
68.26% of random values in a Gaussian distribution will be within one standard
deviation from the mean. 99.74% of the random values will fall within
3 standard deviations (sigma).
Method for generating a Gaussian random distribution:
N = 12 -- the number of intermediate random numbers;
scale = 1/(sqrt(N/12));
sum = sum of N random() numbers;
sigma is the variance;
mean is the average value;
Gaussian value = sigma * scale * (sum - N/2) + mean
The above method will generate a value within N/2 standard deviations
from the mean.
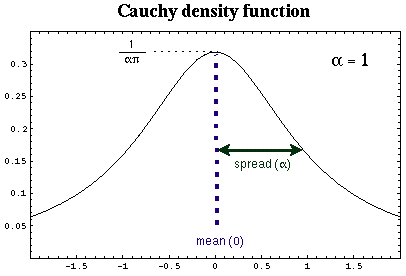
Cauchy Distribution
The density function for the Cauchy distribution approaches 0 slower than
the Gaussian distribution. 50% of random values generated are in the
range of alpha. 99.9% of random values occur within 318.3
alpha.
Method for generating a Cauchy random distribution:
Cauchy value = alpha * tan(pi * random()) + mean // random() != 0.5
Beta Distribution
Weibull Distribution
Poisson Distribution
References:
Dodge, Charles and Thomas Jerse. Computer Music: Synthesis,
Composition, and Performance. New York: Schirmer Books; 1985. pp.
269-278.
Winsor, Phil and Gene DeLisa. Computer Music in C. Blue Ridge
Summit, Pennsylvania: TAB Books; 1991. pp. 177-205.